Chapter 4. Video and Audio Compression

4.1. Lossless Compression Algorithms

Reference: Mark Nelson, "The Data Compression Book", 2nd ed., M&T Books, 1995. QA 76.9 D33 N46 1995

Reference: Khalid Sayood, "Introduction to Data Compression", Morgan Kaufmann, 1996. TK 5102 92 S39 1996

4.1.1 Basics of Information Theory

• indicates the amount of information contained in S_i, i.e., the number of bits needed to code S_i.

• For example, in an image with uniform distribution of gray-level intensity, i.e. p_i = 1/256, then the number of bits needed to code each gray level is 8 bits. The entropy of this image is 8.

• Q: How about an image in which half of the pixels is white (I = 220) and half is black (I = 10)?

A simple example will be used to illustrate the algorithm:

• A top-down approach

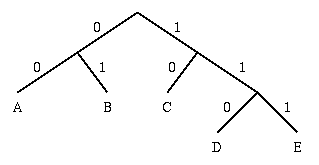
1. Sort symbols according to their frequencies/probabilities, e.g., ABCDE.
2. Recursively divide into two parts, each with approx. same number of counts.

4.1.2 Huffman Coding

• A bottom-up approach

1. Initialization: Put all nodes in an OPEN list, keep it sorted at all times (e.g., ABCDE).

2. Repeat until the OPEN list has only one node left:

(a) From OPEN pick two nodes having the lowest frequencies/probabilities, create a parent node of them.
(b) Assign the sum of the children's frequencies/probabilities to the parent node and insert it into OPEN.
(c) Assign code 0, 1 to the two branches of the tree, and delete the children from OPEN.

Discussions:

• Decoding for the above two algorithms is trivial as long as the coding table (the statistics) is sent before the data. (There is a bit overhead for sending this, negligible if the data file is big.)

• Unique Prefix Property: no code is a prefix to any other code (all symbols are at the leaf nodes)
  --> great for decoder, unambiguous.

• If prior statistics are available and accurate, then Huffman coding is very good.

      In the above example:

      entropy = (15 x 1.38 + 7 x 2.48 + 6 x 2.7 + 6 x 2.7 + 5 x 2.96) / 39
              = 85.26 / 39 = 2.19

      Number of bits needed for Human Coding is: 87 / 39 = 2.23

4.1.3 Adaptive Huffman Coding

(a) The previous algorithms require the statistical knowledge which is often not available (e.g., live audio, video).
(b) Even when it is available, it could be a heavy overhead especially when many tables had to be sent when a non-order0 model is used, i.e. taking into account the impact of the previous symbol to the probability of the current symbol (e.g., "qu" often come together, ...).

The solution is to use adaptive algorithms. As an example, the Adaptive Huffman Coding is examined below. The idea is however applicable to other adaptive compression algorithms.

ENCODER                                 DECODER
-------                                 -------

Initialize_model();                     Initialize_model();
while ((c = getc (input)) != eof)       while ((c = decode (input)) != eof)
  {                                       {
    encode (c, output);                     putc (c, output);
    update_model (c);                       update_model (c);
  }                                       }

• The key is to have both encoder and decoder to use exactly the same initialization and update_model routines.

• update_model does two things: (a) increment the count, (b) update the Huffman tree.
  • During the updates, the Huffman tree will be maintained its sibling property, i.e. the nodes (internal and leaf) are arranged in order of increasing weights (see figure).

  • When swapping is necessary, the farthest node with weight W is swapped with the node whose weight has just been increased to W+1.
    Note: If the node with weight W has a subtree beneath it, then the subtree will go with it.

  • The Huffman tree could look very different after node swapping, e.g., in the third tree, node A is again swapped and becomes the #5 node. It is now encoded using only 2 bits.

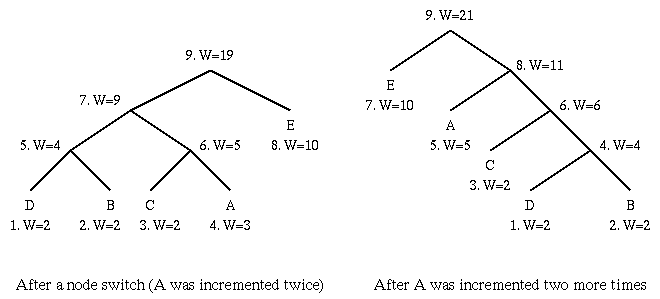
Note: Code for a particular symbol changes during the adaptive coding process.

4.1.4 Lempel-Ziv-Welch Algorithm

Suppose we want to encode the Webster's English dictionary which contains about 159,000 entries. Why not just transmit each word as an 18 bit number?

Problems: (a) Too many bits, (b) everyone needs a dictionary, (c) only works for English text.

• Solution: Find a way to build the dictionary adaptively.

• Original methods due to Ziv and Lempel in 1977 and 1978. Terry Welch improved the scheme in 1984 (called LZW compression). It is used in e.g., UNIX compress, GIF, V.42 bis.

Reference: Terry A. Welch, "A Technique for High Performance Data Compression", IEEE Computer, Vol. 17, No. 6, 1984, pp. 8-19.

LZW Compression Algorithm:

   w = NIL;
   while ( read a character k )
       {
         if wk exists in the dictionary
          w = wk;
         else
           add wk to the dictionary;
           output the code for w;
           w = k;
       }

• Original LZW used dictionary with 4K entries, first 256 (0-255) are ASCII codes.

Example: Input string is "^WED^WE^WEE^WEB^WET".

• A 19-symbol input has been reduced to 7-symbol plus 5-code output. Each code/symbol will need more than 8 bits, say 9 bits.

• Usually, compression doesn't start until a large number of bytes (e.g., > 100) are read in.

   read a character k;
   output k;
   w = k;
   while ( read a character k )    /* k could be a character or a code. */
       {
         entry = dictionary entry for k;
         output entry;
         add w + entry[0] to dictionary;
         w = entry;
       }

• Problem: What if we run out of dictionary space?
  • Solution 1: Keep track of unused entries and use LRU (Least Recently Used)

  • Solution 2: Monitor compression performance and flush dictionary when performance is poor.

• Implementation Note: LZW can be made really fast; it grabs a fixed number of bits from input stream, so bit parsing is very easy. Table lookup is automatic.

Summary

• Huffman maps fixed length symbols to variable length codes. Optimal only when symbol probabilities are powers of 2.

• Lempel-Ziv-Welch is a dictionary-based compression method. It maps a variable number of symbols to a fixed length code.

• Adaptive algorithms do not need a priori estimation of probabilities, they are more useful in real applications.

Further Exploration