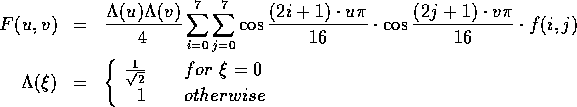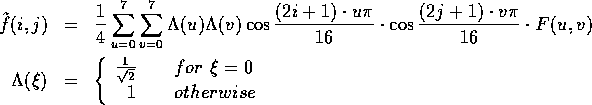4.2. Image Compression -- JPEG

Reference: W.B. Pennebaker, J.L. Mitchell, "The JPEG Still Image Data Compression Standard", Van Nostrand Reinhold, 1993.

4.2.1. Overview of JPEG

What is JPEG?

• "Joint Photographic Expert Group". Voted as international standard in 1992.

• Works with color and grayscale images, e.g., satellite, medical, ...

Motivation

• The compression ratio of lossless methods (e.g., Huffman, Arithmetic, LZW) is not high enough for image and video compression, especially when the distribution of pixel values is relatively flat.

• JPEG uses transform coding, it is largely based on the following observations:
  • Observation 1: A large majority of useful image contents change relatively slowly across images, i.e., it is unusual for intensity values to alter up and down several times in a small area, for example, within an 8 x 8 image block. Translate this into the spatial frequency domain, it says that, generally, lower spatial frequency components contain more information than the high frequency components which often correspond to less useful details and noises.
  • Observation 2: Pshchophysical experiments suggest that humans are more receptive to loss of higher spatial frequency components than loss of lower frequency components.

JPEG overview

• Encoding
  

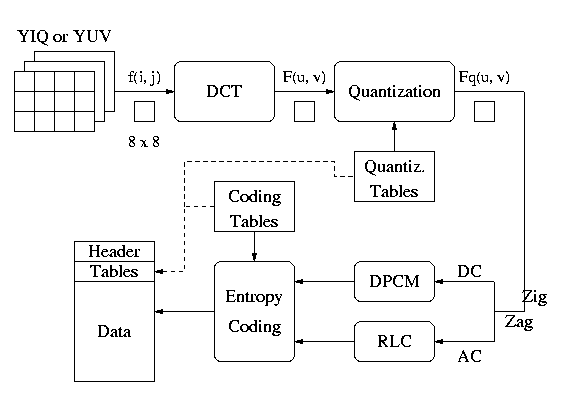
• Decoding -- Reverse the order

4.2.2. Major Steps

• DCT (Discrete Cosine Transformation)
  
• Quantization
  
• Zigzag Scan
  
• DPCM on DC component
  
• RLE on AC Components
  
• Entropy Coding

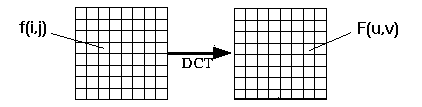
1. Discrete Cosine Transform (DCT)

• From spatial domain to frequency domain:

  

• DEFINITIONS

  Discrete Cosine Transform (DCT):

  

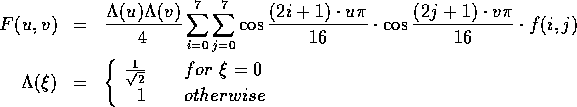
  Inverse Discrete Cosine Transform (IDCT):

  

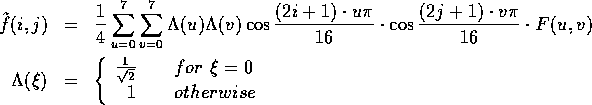
  Question: What are the DC and AC components, e.g., what is F[0,0]?

• The 64 (8 x 8) DCT basis functions:
  

• Why DCT not FFT? -- DCT is like FFT, but can approximate linear signals well with few coefficients.
  

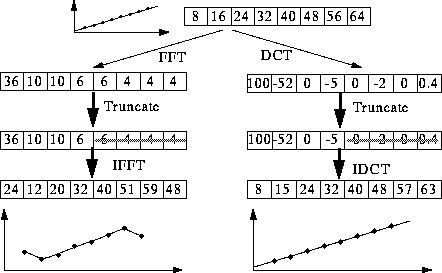
• Computing the DCT
  • Factoring reduces problem to a series of 1D DCTs:

    

    

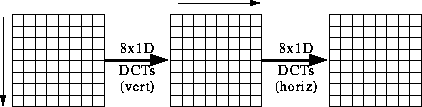
  • Most software implementations use fixed point arithmetic. Some fast implementations approximate coefficients so all multiplies are shifts and adds.

2. Quantization

• F'[u, v] = round ( F[u, v] / q[u, v] ).

  Why? -- To reduce number of bits per sample

  Example: 101101 = 45 (6 bits).
  q[u, v] = 4 --> Truncate to 4 bits: 1011 = 11.

• Quantization error is the main source of the Lossy Compression.

Uniform Quantization

• Each F[u,v] is divided by the same constant N.

Non-uniform Quantization -- Quantization Tables

• Eye is most sensitive to low frequencies (upper left corner), less sensitive to high frequencies (lower right corner)

• The Luminance Quantization Table q(u, v)                 The Chrominance Quantization Table q(u, v)

  ----------------------------------           ------------------------------
  16  11  10  16   24   40   51   61           17  18  24  47  99  99  99  99
  12  12  14  19   26   58   60   55           18  21  26  66  99  99  99  99
  14  13  16  24   40   57   69   56           24  26  56  99  99  99  99  99
  14  17  22  29   51   87   80   62           47  66  99  99  99  99  99  99
  18  22  37  56   68  109  103   77           99  99  99  99  99  99  99  99
  24  35  55  64   81  104  113   92           99  99  99  99  99  99  99  99
  49  64  78  87  103  121  120  101           99  99  99  99  99  99  99  99
  72  92  95  98  112  100  103   99           99  99  99  99  99  99  99  99
  ----------------------------------           ------------------------------
  

  The numbers in the above quantization tables can be scaled up (or down) to adjust the so called quality factor.

  Custom quantization tables can also be put in image/scan header.

3. Zig-zag Scan

• Why? -- to group low frequency coefficients in top of vector.

• Maps 8 x 8 to a 1 x 64 vector
  

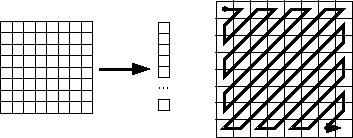
4. Differential Pulse Code Modulation (DPCM) on DC component

• DC component is large and varied, but often close to previous value.

• Encode the difference from previous 8 x 8 blocks -- DPCM

5. Run Length Encode (RLE) on AC components

• 1 x 64 vector has lots of zeros in it

• Keeps skip and value, where skip is the number of zeros and value is the next non-zero component.

• Send (0,0) as end-of-block sentinel value.

6. Entropy Coding

• Categorize DC values into SIZE (number of bits needed to represent) and actual bits.

      ------------------------------------
         SIZE               Value
      ------------------------------------
           1               -1, 1
           2           -3, -2, 2, 3
           3           -7..-4, 4..7
  	 4          -15..-8, 8..15
  	 .                  .
  	 .                  .
  	 .                  .
  	10      -1023..-512, 512..1023
      ------------------------------------
  

  Example: if DC value is 4, 3 bits are needed.

  Send off SIZE as Huffman symbol, followed by actual 3 bits.

• For AC components two symbols are used: Symbol_1: (skip, SIZE), Symbol_2: actual bits. Symbol_1 (skip, SIZE) is encoded using the Huffman coding, Symbol_2 is not encoded.

• Huffman Tables can be custom (sent in header) or default.

4.2.3. A Glance at the JPEG Bitstream

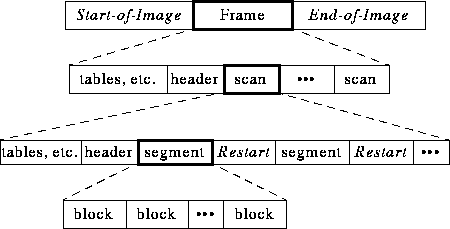
• A "Frame" is a picture, a "scan" is a pass through the pixels (e.g., the red component), a "segment" is a group of blocks, a "block" is an 8 x 8 group of pixels.

• Frame header:
  sample precision
  (width, height) of image
  number of components
  unique ID (for each component)
  horizontal/vertical sampling factors (for each component)
  quantization table to use (for each component)

• Scan header
  Number of components in scan
  component ID (for each component)
  Huffman table for each component (for each component)

• Misc. (can occur between headers)
  Quantization tables
  Huffman Tables
  Arithmetic Coding Tables
  Comments
  Application Data

4.2.4. Four JPEG Modes

• Sequential Mode
• Lossless Mode
• Progressive Mode
• Hierarchical Mode

  ** In "Motion JPEG", Sequential JPEG is applied to each image in a video.

1. Sequential Mode

• Each image component is encoded in a single left-to-right, top-to-bottom scan.

  Baseline Sequential Mode, the one that we described above, is a simple case of the Sequential mode:

  • It supports only 8-bit images (not 12-bit images)
  • It uses only Huffman coding (not Arithmetic coding)

2. Lossless Mode

• A special case of the JPEG where indeed there is no loss.

  Its block diagram is as below:

  

• It does not use DCT-based method! Instead, it uses a predictive (differential coding) method:
  A predictor combines the values of up to three neighboring pixels (not blocks as in the Sequential mode) as the predicted value for the current pixel, indicated by "X" in the figure below. The encoder then compares this prediction with the actual pixel value at the position "X", and encodes the difference (prediction residual) losslessly.
  

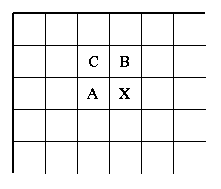
• It can use any one of the following seven predictors :

  Predictor	Prediction
  1	A
  2	B
  3	C
  4	A + B - C
  5	A + (B - C) / 2
  6	B + (A - C) / 2
  7	(A + B) / 2

  Since it uses only previously encoded neighbors, the very first pixel I(0, 0) will have to use itself. Other pixels at the first row always use P1, at the first column always use P2.

• Effect of Predictor (test result with 20 images):
  

  Note: "2D" predictors (4-7) always do better than "1D" predictors.

Comparison with Other Lossless Compression Programs (compression ratio):

-----------------------------------------------------------------
     Compression Program              Compression Ratio        
                               Lena  football    F-18   flowers 
-----------------------------------------------------------------
        lossless JPEG           1.45     1.54     2.29     1.26   
    optimal lossless JPEG       1.49     1.67     2.71     1.33   
       compress (LZW)           0.86     1.24     2.21     0.87   
      gzip (Lempel-Ziv)         1.08     1.36     3.10     1.05   
gzip -9 (optimal Lempel-Ziv)    1.08     1.36     3.13     1.05   
       pack (Huffman coding)      1.02     1.12     1.19     1.00     
-----------------------------------------------------------------

3. Progressive Mode

• Goal: display low quality image and successively improve.

• Two ways to successively improve image:
  1. Spectral selection: Send DC component and first few AC coefficients first, then gradually some more ACs.

  2. Successive approximation: send DCT coefficients MSB (most significant bit) to LSB (least significant bit).
     (Effectively, it is sending quantized DCT coefficients frist, and then the difference between the quantized and the non-quantized coefficients with finer quantization stepsize.)

4. Hierarchical Mode

(From V. Bhaskaran and K. Konstantinides, "Image and Video Compression Standards: Algorithms and Architectures", 2nd ed., Kluwer Academic Publishers, 1997.)

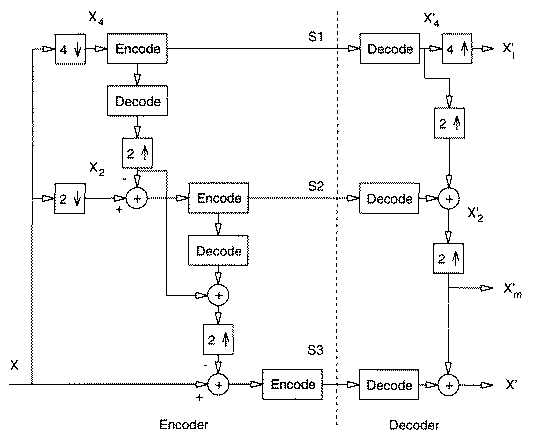
(a) Down-sample by factors of 2 in each dimension, e.g., reduce 640 x 480 to 320 x 240

(b) Code smaller image using another JPEG mode (Progressive, Sequential, or Lossless).

(c) Decode and up-sample encoded image

(d) Encode difference between the up-sampled and the original using Progressive, Sequential, or Lossless.

• Can be repeated multiple times.

• Good for viewing high resolution image on low resolution display.

4.2.5. JPEG 2000

• JPEG 2000 is the upcoming standard for Still Pictures (due Year 2000).
• Major change from the current JPEG is that wavelets will replace DCT as the means of transform coding.
• Among many things it will address:
  • Low bit-rate compression performance,
  • Lossless and lossy compression in a single codestream,
  • Transmission in noisy environment where bit-error is high,
  • Application to both gray/color images and bi-level (text) imagery, natural imagery and computer generated imagery,
  • Interface with MPEG-4,
  • Content-based description.

Further Exploration

Information about JPEG 2000.